It is fairly simple to think about the nails becoming magnets and aligning themselves in the magnetic field. It is also fairly simple to think about them as dominos that "fall" in line with the field. But which is the real explanation, and how would either of them happen?
Both explanations are correct. Magnetic fields exist because somewhere electrons are moving. In the nails, the electrons in the iron atoms are orbiting the nucleus, and each electron is also spinning on its axis. Most materials are not strongly magnetic, because their magnetic poles (caused by spinning electron) are either randomly oriented, or they pair in opposite directions.
If the electrons in an atom (or a molecule) create equal numbers of north and south magnetic poles that cancel each other out, the atom has no magnetic poles. If you bring a magnet near such an atom, the magnetic field causes the electrons in the atom to move. Moving electrons create a magnetic field, and the field they create is opposite to the original magnetic field. The atoms move away from the magnet. Materials that act this way are called diamagnetic materials. The effect is very weak, even in bismuth, which is the most diamagnetic material.
If the electrons in an atom do not create canceling magnets, the atom has a north and a south pole. Normal room temperature causes these atoms to bounce around, and their magnetic poles are randomly oriented. If the atoms are inside a magnetic field, some of them will align with the field. Others will have too much energy and will still bounce around. The amount of energy depends on the temperature, so the colder the atoms are, the more of them will align with the field. Materials that act in this way are called paramagnetic materials. Paramagnetic materials are attracted to magnets, but the effect is weak unless the temperature is very low. Paramagnetic materials also exhibit diamagnetic effects, but the paramagnetic effect is stronger unless the temperature is very high. Aluminum and platinum are paramagnetic.
In  four elements (iron, nickel, cobalt, and gadolinium) the magnetic poles of the atoms stay lined up even at temperatures that thoroughly randomize the poles of other elements. These elements are called ferromagnetic.
four elements (iron, nickel, cobalt, and gadolinium) the magnetic poles of the atoms stay lined up even at temperatures that thoroughly randomize the poles of other elements. These elements are called ferromagnetic.
In the four ferromagnetic elements the magnetic effects are caused by the electrons in the inner orbits. They would align with their poles opposite except for a principle of quantum mechanics called the Pauli exclusion principle. This principle (very loosely interpreted) says that electrons cannot occupy the same space unless they have opposite spins (which means opposite magnetic poles). Two atoms in an element like iron might share an outer electron. This electron will try to align the poles of the inner electrons to be opposite the outer electron. This makes the inner electrons have the same orientation. The inner electrons are thus all aligned the same way, and contribute the magnetic field.
In many paramagnetic materials, the atoms pair up with their north and south poles in opposite directions, canceling each other out. These materials are called antiferromagnetic. Chromium and manganese are antiferromagnetic.
Some materials, called ferrites, are similar to antiferromagnetic materials, but consist of two different magnetic  components, one of which is stronger than the other. This makes them act like ferromagnetic materials, and they are attracted to magnets. The iron ore we have been using is an example of a ferrite. It is a mineral called magnetite, and the natural magnet lodestone is made out of it. The name for this configuration is ferrimagnetism, after the ferrites. Ferrites find many uses in electronics, because they are magnetic, but do not conduct electricity like iron does.
components, one of which is stronger than the other. This makes them act like ferromagnetic materials, and they are attracted to magnets. The iron ore we have been using is an example of a ferrite. It is a mineral called magnetite, and the natural magnet lodestone is made out of it. The name for this configuration is ferrimagnetism, after the ferrites. Ferrites find many uses in electronics, because they are magnetic, but do not conduct electricity like iron does.
Just as electricity travels through some materials better than others, magnetism travels with ease through some materials, and has more difficulty traveling through others. The ability of a material to conduct magnetic flux is called the relative permeability of the material. It is measured relative to the permeability of air, which is assigned a permeability of one. Iron and steel have relative permeabilities between 100 and 9,000. Ferrites have relative permeabilities between 50 and 3,000. The relative permeability of a material can be thought of as the ease with which a material can be magnetized. The higher the relative permeability, the easier it is to magnetize a material.
The lines of force of a magnet, as a group, make up the magnetic flux. The stronger the magnet, the more lines of force it has, and thus the more magnetic flux it has. A typical household magnet has between 100 and 1,000 lines of force. One line of force is called a maxwell. Materials with high relative permeability allow more lines of flux inside them than does the air around them. The flux is thus concentrated in the material. The measure of concentration of flux, measured in lines of force per square centimeter, is the gauss. One gauss is one line per square centimeter. The earth's magnetic field measures about .2 gauss. The superconducting electromagnets used in magnetic resonance imaging range from 5,000 to 15,000 gauss.
When you held the nail close to the magnet, the lines of force of the magnet flowed more easily through the nail than through the air. Just as water seeks the path of least resistance, the magnetic flux sought out the highest relative permeability. Because there would be less resistance if the flux flowed through the entire nail lengthwise rather than through a small part of it crosswise, there is a force on the nail that tends to line it up with the lines of force of the magnet. This is the force that makes it "fall down" parallel to the lines of force. At the same time, the nail is magnetized, and its poles are attracted to the opposite poles of the magnet.
Measures used in permanent magnets.
What makes a good permanent magnet? We want a magnet that has a strongly concentrated magnetic field. We also want a magnet that will stay magnetized. To understand how we measure a permanent magnet's strength and permanence, it is helpful to picture how we make a magnet.
We start with a piece of iron or another ferromagnetic material. We will assume that it is not magnetized when we find it. To magnetize if, we place it in a magnetic field created by another magnet. We will place ours in a field created by an electromagnet, so we can vary the strength of the field and see what happens to the iron.
When the field strength is small, the number of lines of force concentrated in the iron is also small. As the field strength rises, more of the tiny magnets in the iron (called domains) align with the external field. The number of lines of force in the iron rises with the field strength. This continues until all the magnets in the iron line up with the external field. At this point we say the iron is saturated. It cannot hold any more lines of force. As we raise the external field strength, we see no further increase in the number of lines of force in the iron.
Suppose we now start reducing the external field strength. The heat inside the iron at room temperature jostles the tiny magnetic domains inside, and some of them readjust so they do not align with the external field. But some domains stay stuck, aligned with the field. When we completely remove the external field, these stuck domains are left, and we have a permanent magnet.
Suppose we now reverse the external magnetic field, and start gradually increasing its strength. At first the stuck domains resist turning around to align with the external field, and the number of lines of force concentrated in the iron changes only slowly. As the external field gradually overwhelms these stuck domains, they flip over. Eventually the external field is strong enough to flip them all over, and the iron is saturated again (but the poles are now reversed).
If we graph the number of lines of force in the iron against the strength of the external magnetic field, we get a graph that looks like a fat S.
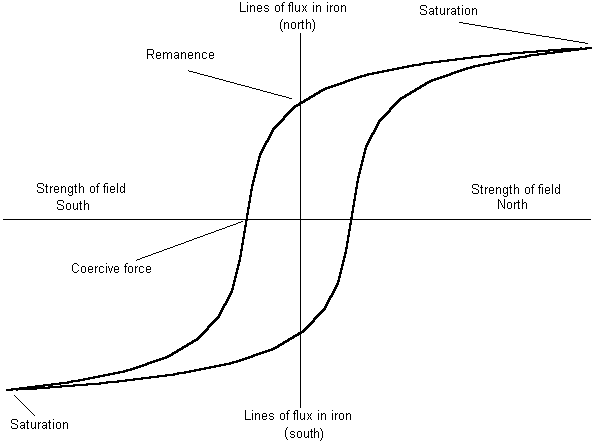
We call the magnetic flux density that remains in the iron when we remove the external field the remanence. We call the strength of the external field needed to demagnetize the iron the coercive force.
What we want in a permanent magnet is a high remanence (measured in gauss) and a high coercive force (measured in oersteds). Radio Shack sells small magnets made from a neodymium-iron-boron alloy that have very high values for remanence and coercivity. The package lists the remanence (which they call by its other name, residual induction) of 10,800 gauss. The coercivity is 9,600 oersteds. Another measurement used to describe permanent magnets is the strength of the external field when the material is saturated multiplied by the number of lines of flux in the material at saturation. This number is the energy product, or the peak energy density, and is measured in gauss oersteds. The Radio Shack magnets have a value of 27 million gauss oersteds. These magnets could be dangerous if they weren't so small. They are less than a quarter of an inch in diameter and about a tenth of an inch high.
Calculating the strength of a magnet
We're going to start with an electromagnet, to look at how magnets are measured, because in some ways it is easier to understand electromagnets first.
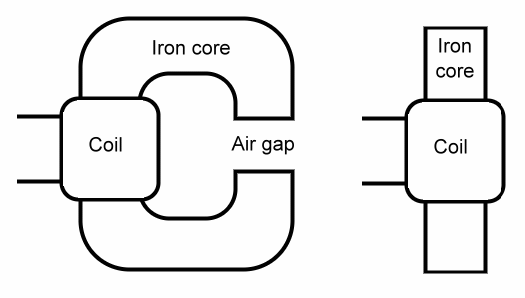
Consider the two electromagnets shown above. The one on the right is a simple coil of insulated copper wire wound around a piece of iron, such as a nail.
The one on the left is the same, but the iron core has been bent around into the shape of the letter 'C', much like a horseshoe magnet.
The left picture makes it easier to see what is called a magnetic circuit. The coil makes a magnet that has a north and a south pole, and the magnetism moves in a circuit from the north to the south, crossing the air gap to get there.
In this respect, a magnetic circuit is similar to an electrical circuit. The flow always goes from one pole to another, like electricity goes from one side of a battery to the other.
Magnetic flux is reluctant to travel through air. It is much easier for it to travel through iron. We say that air has a high reluctance, and iron has a low reluctance. This is similar to resistance in an electrical circuit.
In an electrical circuit, we have Ohm's Law, which says that voltage is equal to current times resistance. In a similar way, magnetomotive force is equal to the magnetic flux times the reluctance. Thus magnetomotive force is similar to voltage, and magnetic flux is similar to current.
The magnetomotive force is produced by the coil. It is measured in ampere-turns, the electrical current in the coil, measured in amperes, times the number of turns of wire in the coil.
We can calculate the reluctance of the iron core and the air gap if we know the length, the area, and the permeability of the iron and the air. Just like in calculating the resistance of a wire, the reluctance goes down if the cross sectional area gets bigger, and the reluctance goes up if the length gets longer.
The permeability is a constant that depends on the material.
The permeability of free space, also known as the magnetic constant, is 0.00000125663706 meters kilograms seconds-2 amperes-2. Rather than remember all of those clumsy units, we have a simpler unit, the henry, and we measure permeability in henries per meter.
For simplicity, we will refer to permeability as the Greek letter "mu" μ, and the permeability of free space as "mu sub zero", μ0, and say that air is 1 μ0 and iron is about 1,000 μ0.
The formula for reluctance is the length divided by the product of the permeability and the area.
We have an iron core that is one centimeter square in area, and is 15 centimeters long, bent into a 'C' shape with a 1 centimeter air gap. The reluctance of the iron core is 15 centimeters divided by 1,000 times one square centimeter. The reluctance of the air gap is 1 centimeter divided by 1 times 1 square centimeter. We add the two together to get the reluctance of the entire magnetic circuit.
The iron core comes to about 1.5 henries per meter, and the air gap comes to about 100.
Now we can calculate the magnetic flux in our magnetic circuit. Flux is measured in Webers.
Suppose we have just one loop in our coil, and we have 1 ampere of current going through the coil. We thus have 1 ampere-turn of magnetomotive force.
Dividing one ampere by the total reluctance of the circuit, we get 0.0000000123806607 webers.
That is the total flux. We also measure the flux density, that is, the flux per square meter (called B). Webers per square meter is a unit known as the tesla. We have 0.000123806607 teslas in the air gap of our our one-turn electromagnet.
If we had 5,000 turns of wire in our coil, we would have 5,000 times the flux density, or 0.619033035 teslas in the air gap of our our 5,000-turn electromagnet.
Our little 'C' shaped magnet has room for a coil about 3 centimeters long and 4 centimeters wide. If we use 28 gauge wire (0.33 millimeters in diameter), we can get about 90 turns per layer, and about 120 layers, for a total of about 10,000 turns. 28 gauge wire can handle 1.4 amperes of current (more if we cool the coil with water or liquid helium). So, our magnet is now up to 1.7 teslas, and runs very hot.
The average length of one turn of wire in our coil is about 10 centimeters. We have 10,000 turns, so that is one kilometer of wire. A kilometer of 28 gauge wire has 213 ohms of resistance. To get 1.4 amperes through 213 ohms of resistance takes just under 300 volts.
We have calculated flux and flux density of our coil. Now we need the magnetic field strength. We start with the magnetomotive force we discussed earlier, which is simply the number of ampere-turns in our coil. We have 1.4 amperes, and 10,000 turns, so we have 14,000 ampere-turns of magnetomotive force. The magnetic field strength is the magnetomotive force divided by the length of the magnetic circuit, which in our example is 16 centimeters. So the magnetic field strength (called H) is 14,000 ampere-turns/16 centimeters, or 875 ampere-turns per centimeter.
So far we have been discussing the 'C' shaped magnet. The simpler magnet works the same way, but the length of the iron core is now 8 centimeters, and the length of the air gap has increased considerably.
If we assume for the moment that the air gap is now the same length as the iron core (each is now 8 centimeters), we get 0.22 teslas, and it still runs very hot. The magnetomotive force has not changed (still 14,000 ampere-turns), but the flux has dropped considerably, since the extra 7 centimeters of air gap has a lot more reluctance.
However, the air gap is actually larger than 8 centimeters. The magnetic flux in the iron stays pretty much entirely in the iron. This is because up to the saturation point of the iron, it is a very good conductor of magnetic flux. Air, on the other hand, is a poor conductor, and the flux spreads out over a large area, making the average path length larger.
Permanent magnets have the same units of strength and flux. A permanent magnet with a flux density of 1.32 tesla (such as an N42 neodymium-iron-boron magnet) has the same flux density as our 'C' shaped magnet if we reduce the current to 1.067 amperes.
The same permanent magnet has a magnetic field strength of 11,000 ampere-turns per centimeter. This is 12.5 times as strong as our electromagnet. We would need to add more current or more windings, or reduce the length of the magnetic circuit to get the same strength as the permanent magnet. Of course, we could do some combination of the three.
In a practical electromagnet, this is difficult. Reducing the length of the circuit means that there will be less room for the coil. Adding turns means we need a longer magnetic circuit to hold them. Adding current means that we need a fatter wire, which means we get fewer turns in the same space. You can see why people choose to cool their electromagnets with water or cryogenic liquids. It allows you to use more current without increasing the diameter of the wire.
What the magnetic field strength means in terms of our permanent magnet is simple. It is the strength of an electromagnet needed to demagnetize the permanent magnet.