The photo above shows our tiny computer connected to a thermistor and a 10,000 ohm resistor.
A thermistor is a device whose resistance changes with temperature in a well-defined way. We can use it to tell how hot or cold something is.
Schematically, it looks like this:
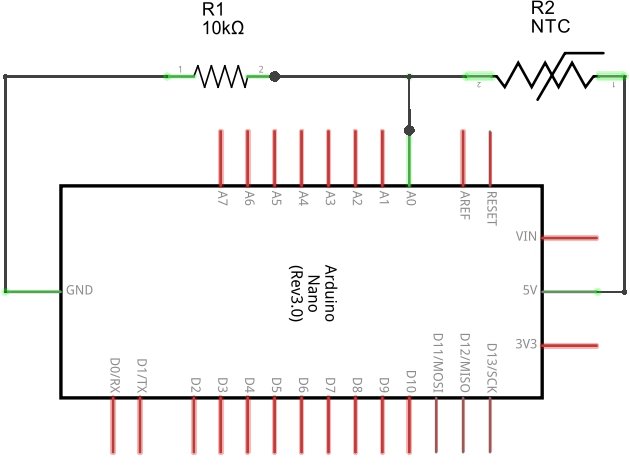
The thermistor has a resistance that centers around 10,000 ohms. We add a normal resistor of the same value in series with the thermistor, and attach the other ends of each to power and ground, so the power goes through both resistors to ground.
This arrangement is called a voltage divider. If both resistances are the same, the little computer will see 2.5 volts on the A0 pin. If the resistance of the thermistor goes down, the voltage on pin A0 will go up. Our thermistor is a negative temperature coefficientthermistor, so the resistance goes down (by 4.4 ohms per degree Celsius).
We can read the output with a simple program:
void
setup()
{
Serial.begin( 115200 );
}
void
loop()
{
Serial.println( analogRead( A0 ) );
delay( 1000 );
}
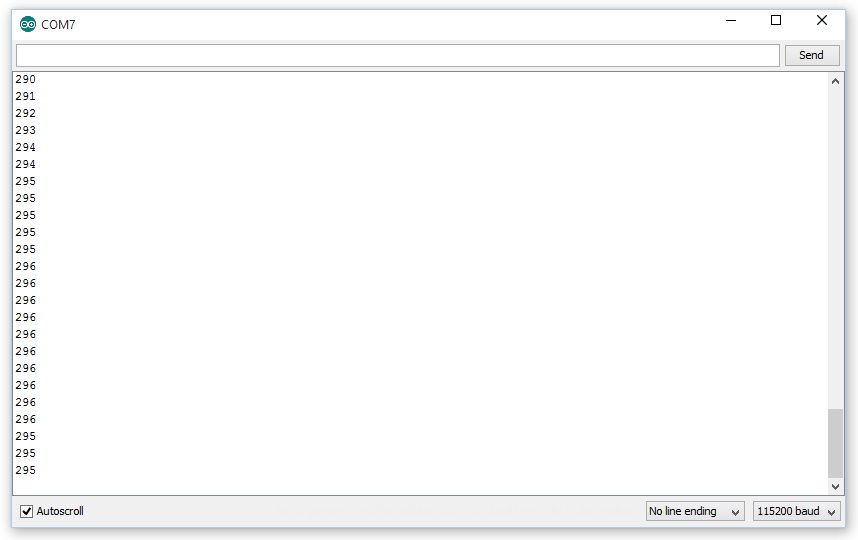
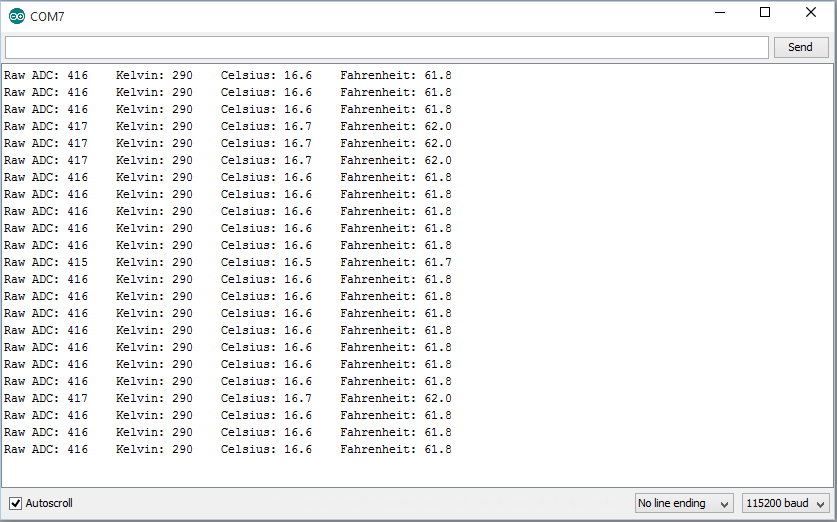
On the serial monitor, you will see a number (probably close to 500) printed every second.
That is what we call the raw ADC value, the value we get from the computer's Analog to Digital Converter. It does not look much like a usable temperature. It isn't Celsius or Fahrenheit, or even Kelvin. We could convert it to a voltage, but that is hardly an improvement.
But we can look up the characteristics of thermistors, and come up with a mathematical formula that converts the raw ADC value into a temperature. A program to do that looks like this:
# include <math.h>
double
kelvin( int value )
{
double Temp = log( 10000.0 * ( ( 1024.0 / value - 1 ) ) );
return 1.0 / ( 0.001129148 + ( 0.000234125
+ ( 0.0000000876741 * Temp * Temp ) ) * Temp );
}
void
setup()
{
Serial.begin( 115200 );
}
void
loop()
{
int raw_adc = analogRead( A0 );
double k = kelvin( raw_adc );
Serial.println( k, 0 );
delay( 1000 );
}
Now we see the temperature printing out in Kelvins:
At this point we should go over a few new concepts used in this program. The first line, for example, says to include a file called "math.h" into our program at this point. That file is needed because it defines the function log() , which we use in our function kelvin(), which comes next.
Up until now we have been ignoring the word void that we have been seeing above our functions, but never discussed. Functions can return values. When they don't return a value, we declare them as returning "void". When they do return a value, we have to say what the type of the value is. In C++, there are many types. There are integers, characters, classes, floats, doubles, and several more. In this case, we want to return adouble. A float is a type of number that has a floating decimal point (as opposed to an integer, which can only hold integer values). A double is a float with twice the precision, and takes up twice as much memory.
So our kelvin() function is going to return a number that can express fractions (decimals), and we want a lot of precision.
Inside the kelvin() function is a lot of scary arithmetic and long numbers. That is just the code that expresses the Steinhart–Hart equation, the formula for converting the raw ADC value into degrees Kelvin. The long numbers are the values of A, B, and C in that equation for our typical thermistor. The plus signs and minus signs are familiar from arithmetic. The slash (/) and asterisk (*) are used for division and multiplication.
The rest of the program should look familiar, except for the line that calls the functionkelvin(), passing in raw_adc as the argument, and putting the return value into a temporary variable called "k", which has a double precision floating point type:
double k = kelvin( raw_adc );
Most of us don't commonly use the Kelvin temperature scale. But with a little arithmetic, we can convert degrees Kelvin to degrees Celsius, or to degrees Fahrenheit.
Our next program does that, by adding a few lines of code in the loop() function:
# include <math.h>
double
kelvin( int value )
{
double Temp = log( 10000.0 * ( ( 1024.0 / value - 1 ) ) );
return 1.0 / ( 0.001129148 + ( 0.000234125
+ ( 0.0000000876741 * Temp * Temp ) ) * Temp );
}
void
setup()
{
Serial.begin( 115200 );
}
void
loop()
{
int raw_adc = analogRead( A0 );
double k = kelvin( raw_adc );
Serial.print( "Raw ADC: " );
Serial.print( raw_adc );
Serial.print( " Kelvin: " );
Serial.print( k, 0 );
Serial.print( " Celsius: " );
Serial.print( k - 273.15, 1 );
Serial.print( " Fahrenheit: " );
Serial.println( (k - 273.15) * 1.8 + 32, 1 );
delay( 1000 );
}
One thing to notice here -- we give println() two arguments instead of just one (arguments to functions are separated by commas, just like in mathematics). The second argument in this case says to print one decimal place instead of the default two decimal places, when printing floating point numbers. Two decimal places would give us four significant digits, but we only had three in our original raw_adc value. A fourth digit would give us the false impression that we knew the temperature more accurately than we actually do.
Let's clean up our program and make a nice Temperature class that we can more easily use in other programs.
Here is our class Temperature:
class Temperature
{
int raw_adc;
public:
int raw( int pin ) { return raw_adc = analogRead( pin ); }
int raw( void ) { return raw_adc; }
double
kelvin( void )
{
double Temp = log( 10000.0 * ( ( 1024.0 / raw_adc - 1 ) ) );
return 1.0 / ( 0.001129148 + ( 0.000234125
+ ( 0.0000000876741 * Temp * Temp ) ) * Temp );
}
double celsius( void ) { return kelvin() - 273.15; }
double fahrenheit( void ) { return kelvin() * 1.8 - 459.67; }
};
This class contains the method kelvin(), but also celsius(), fahrenheit(), and two forms of raw().
The first raw() method takes an argument telling it which pin the thermistor is attached to. It reads the analog value at that pin, and stores it in the variable raw_adc, and returns the value to the caller of the method.
The second raw() takes no argument, and simply returns the stored raw_adc value. When we create two functions with the same name, but different arguments, we say we are overloading the name.
Any time we want to read the temperature, we first need to call raw( A0 ). Then we can call kelvin(), celsius(), or fahrenheit() to convert the raw data to a temperature.
To declare an instance of our class, we add this line:
Temperature temperature;
Now our loop() function looks a little cleaner:
void
loop()
{
Serial.print( "Raw ADC: " );
Serial.print( temperature.raw( A0 ) );
Serial.print( " Kelvin: " );
Serial.print( temperature.kelvin(), 0 );
Serial.print( " Celsius: " );
Serial.print( temperature.celsius(), 1 );
Serial.print( " Fahrenheit: " );
Serial.print( temperature.fahrenheit(), 1 );
delay( 100 );
}
Calibration
By adding a little bit of code to collect a couple hundred samples and calculate the mean and standard deviation, we can use an ice bath to calibrate our thermometer.

A properly built ice bath has some important characteristics. It must have ice all the way to the bottom of the container, otherwise there will be water that is not at zero Celsius (32 Fahrenheit) at the bottom. It should be almost full of water. There should be enough ice above the water to ensure that the ice touches the bottom. It should be left for a few minutes to ensure that the water is at zero Celsius. Lastly, the temperature probe should be stirred in the ice-water bath during the measurement, to ensure that it is not touching the ice, which is below zero.
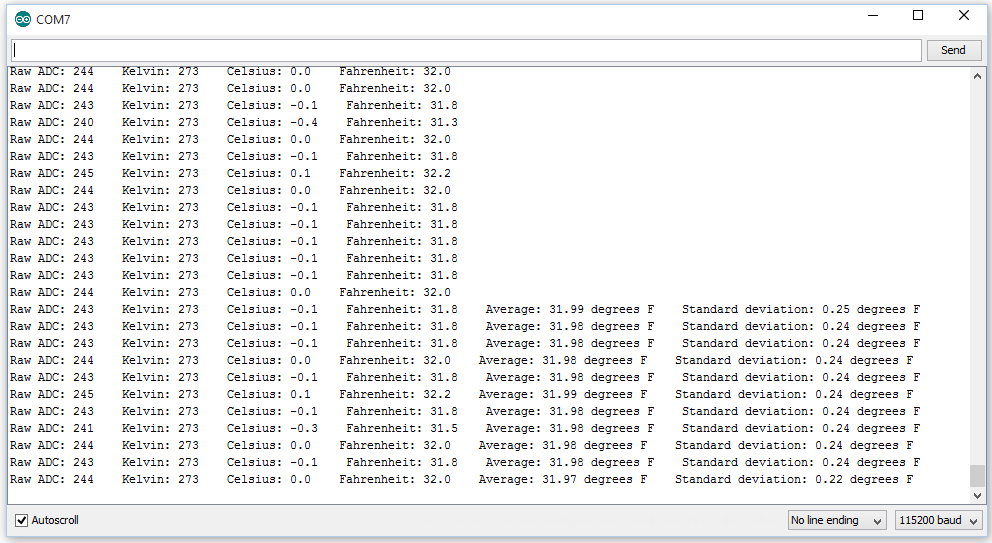
The modified program will print out the temperature until there are enough readings to calculate the standard deviation and mean. At that point, it prints out both of those readings with each line:
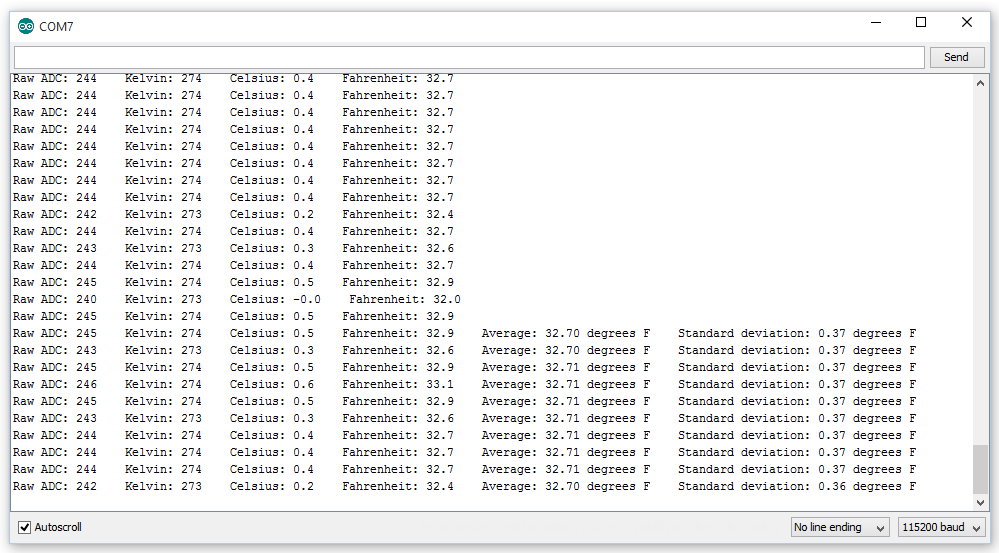
In this case, we see that the mean is 32.71 degrees, and the standard deviation is 0.37 degrees.
The "true" temperature is somewhere between 32.34 and 33.08 degrees.
Since we know the temperature is 32 degrees, we can tell that our thermometer is reading high by at least 0.34 degrees Fahrenheit.
If we subtract 0.71 degrees from each reading, our average reading for the ice-water bath should be around 32 degrees, plus or minus 0.37 degrees.
Notice that we are printing temperatures as if we could tell the difference between 32.6 and 32.7 degrees. But we don't really have that kind of accuracy or precision. We can say that we have 95% confidence that when the average temperature reads a certain value, the actual temperature falls between -0.37 and +0.37 of that value. That corresponds to 2 deviations from the mean. We have a 99.7% confidence that the average temperature falls within 3 deviations from the mean, or -0.555 and +0.555 degrees from the reading we get from our thermometer.
With that information, we can say that (after adding our calibration offset) we have a thermometer that is accurate to about a degree Fahrenheit.
After calibration, here is our ice-water bath temperature data: