We can modify the temperature collection programs to collect data on our water bath. This is important because it helps us pick the three tuning parameters that our PID controller needs. We can pick some arbitrarily, and look at the graph of how the system reacts, and then modify the parameters to make the water bath temperature come to the target quickly, but minimize overshoot and oscillation.
The program to read the USB serial data from the tiny computer and store it in a database is here. It is the same as our earlier data storage program, but this time we report not just the temperature, mean, and standard deviation, but also the value of how much current was sent to the heater, and what the current value of the Integral is in the PID controller, and what the target temperature is.
Similarly, the program to graph the data is also only a slight modification of an earlier program.
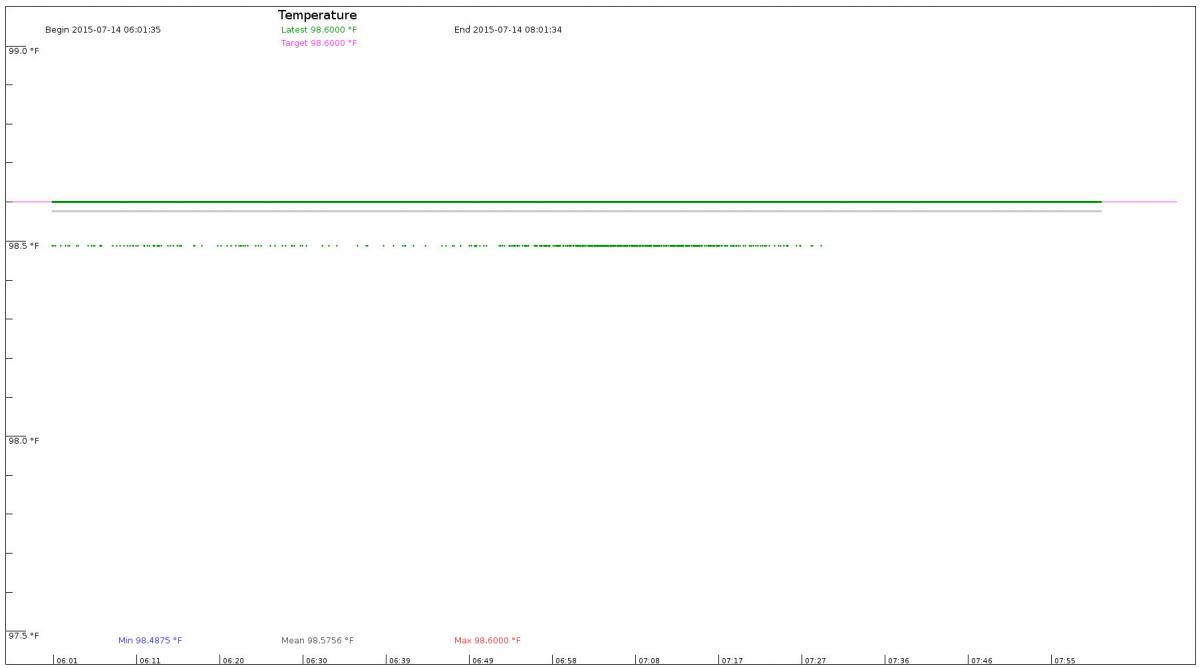
The graph presents the last two hours of water bath temperature (click on the image to get a larger picture):
What we see is the way the PID controller reacts to small changes in the temperature of the room outside the Styrofoam box. As the room cools, the heater can't keep up with the temperature loss. The temperature drops by the smallest amount that we can measure (0.0625 degrees Celsius, or 0.1125 degrees Fahrenheit). The PID controller sends more current to the heater, and the temperature is restored to 98.6 degrees. The running average (the gray line) shows the history of previous temperatures, and in this case shows that the earlier temperatures were lower (on average).
The graph makes it easier to tune the PID controller. Those three parameters were chosen by looking at the graph and changing the parameters based on what we saw. When the graph showed the temperature moving towards the target too slowly, we increased the first parameter (the Proportional coefficient). If the graph showed the temperature leveling off somewhere under or over the target temperature, we increased the Integral parameter. If the graph showed oscillations, we knew that the Proportional and Integral numbers were too high, or the Derivative was too low. If increasing the Derivative parameter didn't fix the oscillations, we backed off on the Proportional and Integral parameters until the oscillations stopped.